Two Sum - Leetcode #1 Short & Simple Solution

Hello Code Recipian! Welcome back to another article on leetcode problem solutions. In this article we will be solving leetcode problem no. 1 Two Sum.

This problem is one of the most popular questions on leetcode and also a popular choice in coding interviews. Once you have a good understanding of this problem, it should help you solve advanced level problems like three sum which is an extension of the two sum problem.

Problem Statement: Two Sum

Consider you are given an array of integers nums and an integer target, return indices of two numbers in the array such that they add up to the given target.

You may assume that each input would have exactly one solution. Also, you cannot use the same element twice. You are allowed to return the answer in any order.

Example

​

Example 1:

Input: nums = [7,2,13,11], target = 9
Output: [0,1]
Explanation: Element at index 0 i.e. 7 and element at index 1 i.e. 2 when added give target = 9.

Example 2:

Input: nums = [7,3,5], target = 8
Output: [1,2]

Solution

Let us try to understand the problem statement first. Here we are given an array of integers nums and another integer called target. We are asked to write an algorithm which returns indices of two elements in this array, such that, when we add the the numbers at these two indices it should be equal to the given target sum.

For instance, in example 1 [7, 2, 13, 11] is the given array and the given target sum = 9. If we take a look at the given array, the pair which adds to the target sum 9 is (7,2) i.e. 7+2 = 9. So, our algorithm should return (0,1) as the result because these are the indices of elements 7 and 2 respectively in the given nums array.

Similarly, for the array in example 2 [7, 3, 5] output is (1,2) because these are the indices of elements 3 and 5 respectively which add up to the target sum 8.

It is possible to solve this problem in linear time. The idea is to use a hashmap to store the indices of the elements that are already visited. Let's see how this algorithm works.

Algorithm

Below is a step-by-step explanation for the working of the algorithm:

1. Initialization:

   Create a hashmap numberIndexMap which accepts an integer key and value. This hashmap is used to store the indices of the numbers we have encountered so far in our previous iterations.

2. Find indices that add up to the given target:

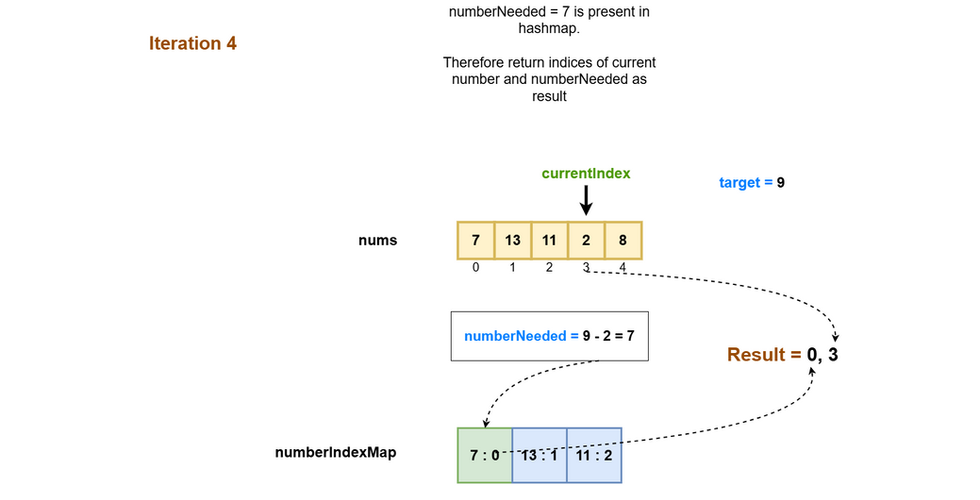
   Iterate through each element in the given array starting from the first element. In each iteration we perform the following steps:

   1. Calculate the number needed to achieve the target sum using the current number. number needed = target - current number

   2. Check if the number needed is already present in hashmap, i.e. check if we have already encountered the needed number in one of our previous iterations.

      1. If yes, we have found the numbers that add up to the given target (i.e. current number, needed number). Therefore, return the indices of current number and needed number as result.

      2. If no, add the current number along with its index to the numberIndexMap. This will allow us to verify if we have come across this number in future iterations.

   3. Repeat steps a and b for each element in nums array until we find the result.

Simulation

Below diagram shows a pictorial depiction of the working of the algorithm:

Want to master coding? Looking to upskill and crack interviews? We suggest you check out these specially designed courses:

1. Udemy Video Tutorials - Available at 95% off

2. System Design Interview Complete Guide

3. Cracking The Coding Interview - Most Preferred Book For Coding Interviews

4. Data Structures And Algorithms - A Complete Guide 

5. Learn In-Demand Tech Skills And Stay Ahead Of Others

Video Explanation

If you are looking for a video explanation for Two Sum problem, you can checkout the video in our Code Recipe YouTube channel:

Code

Go Solution

Python Solution

Java Solution

JavaScript Solution

TypeScript Solution

C++ Solution

C# Solution

PHP Solution

Kotlin Solution

Swift Solution

Ruby Solution

C Solution

Rust Solution

Complexity Analysis

Time Complexity

The running time complexity of this solution is O(n) since we would have to go through all array elements in the worst case. The worst case occurs when we have to traverse till the end of array to get the result.

Note: The worst case for checking if an element exists in hashmap can go up to O(n^2) in the worst case if there are collisions. However, most modern languages have a pretty robust implementation for hashmap and hence the chances of collision is minimal.

So, in general we can say the overall time complexity of the solution is O(n).

Space Complexity

Also the auxiliary space required is O(n) since we store the array elements in hashmap and in the worst case we would end up storing all values in nums in hashmap.

That brings us to the end of this article. We sincerely appreciate the time you have taken to read through it. If there are any questions, feel free to ask them in the comments below. We're here to help and will gladly answer your queries.

If you enjoyed this article, please subscribe to our website and Youtube channel. Your support inspires us to create more such articles in the future.

Don't forget to delve into more such fascinating articles from Code Recipe in our blogs section. There's a wealth of knowledge waiting for you there!

Code Recipe Limited Time Offer: Get 100% discount on Code Recipe Membership Plan. Join now and get exclusive access to premium content for free. Hurry! Offer only available for a limited time - Join now.

Follow us: YouTube, Facebook, Twitter, LinkedIn, Tumblr, Instagram.